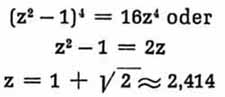Der Allbandkreis
Für Kurzwellengeräte - vorwiegend beim Senderbau - will man häufig mit einem Abstimmkreis einen großen
Frequenzbereich überstreichen, ohne daß eine komplizierte Spulenschaltung notwendig ist. Diesem Verlangen
trägt der Allband- oder auch Multibandkreis Rechnung. Der in Amateurkreisen geprägte Name besteht nicht ganz zu
Recht, denn der Kreis zeigt nicht nur auf verschiedenen Bändern Resonanz, sondern liefert bei entsprechender Bemessung
der Schaltung eine lückenlose Abstimm-Möglichkeit über einen sehr großen Frequenzbereich. Es bereitet
z. B. keine Schwierigkeiten, mit einer Induktivität von nur 2,5 µH und einem normalen Drehkondensator von rund 500 pF
den Bereich von ungefähr 2 MHz bis 30 MHz zu überstreichen, wobei als Drehkondensator-Anfangskapazität
(einschließlich Schaltkapazitäten) 30 pF angesetzt wurden. Für dieses große Frequenzverhältnis
von 1:15 wäre normalerweise eine Drehkondensator-Variation von 1:225 erforderlich, das sind 30...6750 pF.
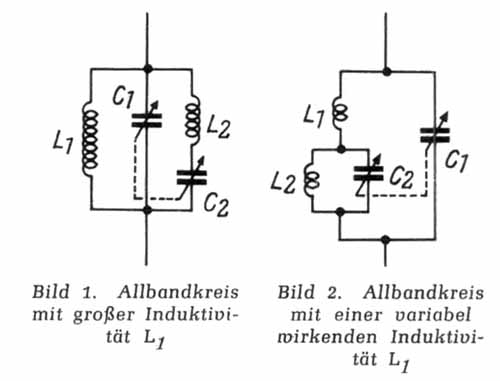
Bekannt ist der Allbandkreis nach Bild 1, wobei L1 eine große und L2 eine kleine Induktivität darstellen. L1 wirkt
daher bei hohen Frequenzen als Drossel, und die Resonanz wird vorwiegend durch L2 bestimmt. Die beiden Drehkondensatoren
liegen hierbei gewissermaßen in Serie. Bei niedrigen Frequenzen sind die Verhältnisse praktisch umgekehrt, d. h.
L1 dient als Abstimmspule und die beiden Drehkondensatoren liegen parallel. L2 kann wegen der niedrigen Induktivität in
diesem Fall vernachlässigt werden.
Eine etwas abgeänderte Schaltung mit einigen interessanten Einzelheiten bringt Bild 2.
Die linke Seite des Kreises, bestehend aus der Serienschaltung von L1 und dem Parallelkreis L2/C2, können wir als
variable Induktivität ansehen, denn der Parallelkreis kann einmal induktiv wirken (elektrische Vergrößerung
von L1), zum anderen aber auch kapazitiv (elektrische Verkleinerung von L1), je nach Frequenz und eingestellter
Kapazität C2 bzw. der Größe von L2.
Bei Resonanz des Allbandkreises nach Bild 2 muß der Wechselstromwiderstand X von C1 gleich sein dem
Wechselstromwiderstand der linken Seite. Gleichungsmäßig ergibt das:
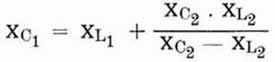
Im Gegensatz zum Allbandkreis nach Bild 1 machen wir L1 = L2, was die Rechnung sehr vereinfacht, zumal auch C1 = C2 ist
(Gleichlauf). Wir erhalten also:
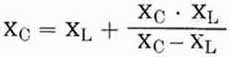
Diese Gleichung lösen wir nach Xc auf, wobei wir auf die quadratische Gleichung stoßen
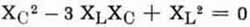
so daß wir für Xc gleich zwei Werte erhalten, nämlich
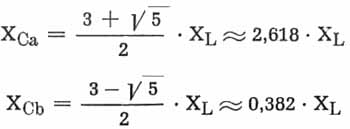
Oder in C- und L-Werten ausgedrückt :

Ferner ergibt sich das Verhältnis
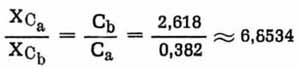
Wie uns diese Formeln zeigen, erhalten wir bei einer bestimmten Frequenz mit zwei verschiedenen C-Werten Resonanz. Hierbei
kann allerdings der eine C-Wert so klein oder auch so groß sein, daß er nicht mehr in den Bereich unseres
Drehkondensators fällt, wie wir später noch sehen werden.
Außerdem erkennen wir, daß der Allbandkreis bei einem fest eingestellten C-Wert für zwei verschiedene
Frequenzen in Resonanz sein muß. Die Überprüfung einer Versuchsschaltung mit einem Grid-Dipmeter
bestätigt uns diese Tatsache. In der Praxis kann diese Eigenschaft u. a. in Sender-Vervielfacherstufen ausgenutzt werden,
wenn z. B. neben der Grundfrequenz von 7 MHz gleichzeitig auch die dritte Harmonische, nämlich die Frequenz 21 MHz,
übertragen werden soll.
Die beiden Resonanzfrequenzen fa und fb verhalten sich in unserem Fall, also wenn L1 = L2 ist, wie

wobei
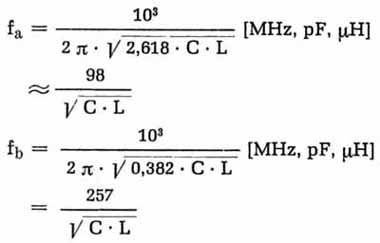
Wählt man die beiden Spulen nicht gleich groß, so erhält man unter Verwendung von Formel bei Gleichlauf
von C1 und C2, also
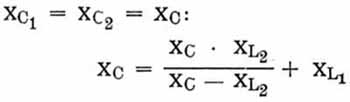
Nach Xc aufgelöst, ergibt sich:
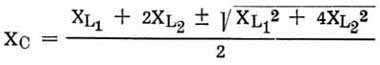
Zur Vereinfachung der Formel setzen wir XL2 als Vielfaches von XL1 an, also
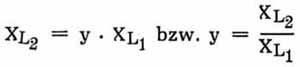
Das ergibt für Xc :
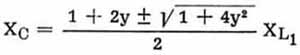
bzw.

Um die beiden Resonanzfrequenzen zueinander in ein bestimmtes Verhältnis bringen zu können, löst man die
Gleichung nach y auf. Zur Vereinfachung wird gesetzt :
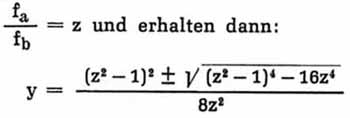
Beispiel: Man will mit einem Abstimmkreis gleichzeitig auf 7 und 21 MHz Resonanz erzielen (Grundfrequenz und
Verdreifachung), z ist also 3. Setzen wir in die Gleichung für z den Wert 3 ein, so ergibt sich für
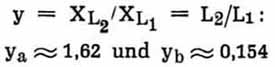
Man erhält also für y gleich zwei Werte, d. h. man kann die geforderten Bedingungen erreichen durch L2 = 1,62
• L1 oder durch L2 = 0,154 • L1. In der Praxis wird sich in den meisten Fällen nur einer dieser beiden Werte verwenden
lassen, da die Induktivitäten der Frequenz und dem C-Wert angepaßt werden müssen.
Die untere Grenze für 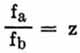 ist gegeben, wenn der Ausdruck unter der Wurzel "Null" wird,
also wenn
ist gegeben, wenn der Ausdruck unter der Wurzel "Null" wird,
also wenn
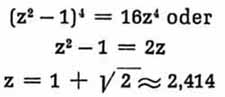
Wir erhalten dann für y = 0,5.
Eine Frequenzverdopplung (z = 2) ist zur Grundfrequenz also nicht möglich, wenigstens nicht, wenn C1 = C2 ist, da der
Wert unter der Wurzel negativ bzw. der Wurzelwert imaginär wird.
Allbandkreis für den Amateurgebrauch
Für den Amateurgebrauch wählen wir am besten den Allbandkreis so, daß L1 = L2 = L. Es ergeben sich
dadurch einfache Rechnungen, wobei die zwei Formeln
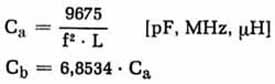
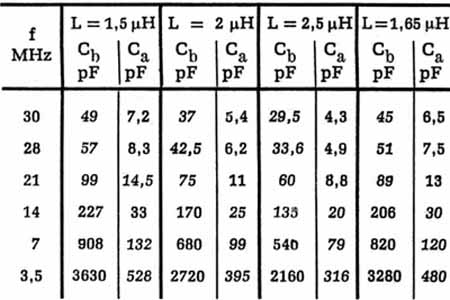
im allgemeinen genügen. In nachstehender Tabelle werden für ein paar L-Werte die zugehörigen Ca bzw. Cb
- Werte angegeben.
Die günstigsten C-Werte wurden in schräger Schrift gesetzt. Welcher L-Wert am günstigsten ist, hängt von
der Anfangskapazität des Drehkondensators plus den üblichen Schaltkapazitäten ab. Günstig ist vor allem
auch L = L1= L2 = 2,5 µH, da wir hierbei mit einem Drehkondensator von etwa 2 x 300 pF auskommen. Sind Anfangskapazität
des Drehkondensators plus Schaltkapazitäten nicht größer als 20 pF, dann erscheint bei dieser Induktivität
das 20-m-Band an erster Stelle beim Eindrehen des Drehkondensators.
Dann folgen 10-m-, 15-m-, 40-m-Band, anschließend nochmals 20 m, und am Ende des Drehkondensators 80 m.
Die Verwendung des Allbandkreises beschränkt sich nicht nur auf Sender-Endstufen oder -Vervielfacherstufen, er kann
auch in Empfänger-Vorstufen verwendet werden, wobei unter Benutzung eines Vierfach-Drehkondensators sogar zwei Stufen
im Gleichlauf betrieben werden können.

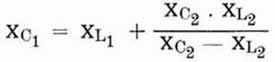
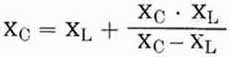
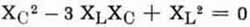
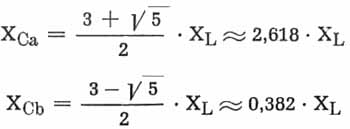

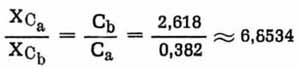


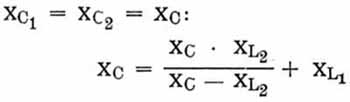
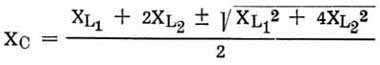
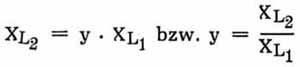
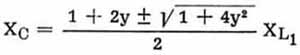

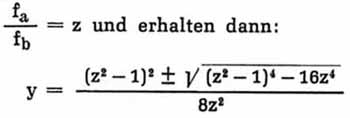
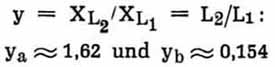
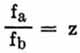 ist gegeben, wenn der Ausdruck unter der Wurzel "Null" wird,
also wenn
ist gegeben, wenn der Ausdruck unter der Wurzel "Null" wird,
also wenn