Der Ausgangstransformator - Berechnung in Formeln und Nomogrammen
Nachfolgend soll weniger ein neuer als vielmehr ein möglichst einfacher Weg zur Ermittlung aller Daten eines dem
jeweiligen Verwendungszweck angepaßten Ausgangstransformators aufgezeigt werden. Daher werden zunächst die
für die Berechnung anzuwendenden Formeln diskutiert, und im Anschluß daran sei an Hand einiger Nomogramme gezeigt,
wie man auch ohne Berechnung sehr schnell zum Ziel kommen kann. Die bei Verwendung der Nomogramme erreichbare Genauigkeit
genügt für alle Zwecke der Praxis vollständig, zumal bei Ausgangstransformatoren wesentlich größere
Toleranzen zulässig sind .als z. B. bei Netztransformatoren.
Die für die Übertragung der tiefsten Frequenz fu (Kreisfrequenz = 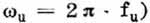 wesentliche Induktivität L der Primärwicklung des Ausgangstransformators errechnet sich nach der folgenden Formel
wesentliche Induktivität L der Primärwicklung des Ausgangstransformators errechnet sich nach der folgenden Formel

in H, sofern Ri und Ra der innere Widerstand der Endröhre bzw. der
äußere (Belastungs-) Widerstand (beide Werte können für die jeweilige Endröhre den Röhrenlisten
entnommen werden) in W ist und die tiefste in Betracht kommende Kreisfrequenz wu in Hz eingesetzt wird. Der für wu einzusetzende Wert richtet sich in der Hauptsache nach dem benutzten Lautsprecher. Daher
hat es keinen Sinn, den Ausgangstransformator z. B. für fu = 30 Hz zu berechnen, wenn der vorhandene
Lautsprecher vielleicht schon bei 100 Hz kaum noch nennenswert abstrahlt.
Die zweite wichtige Größe ist der Querschnitt FK des Eisenkernes. Hierfür
gilt in guter Annäherung die folgende Formel

wobei FK in cm² erhalten wird, wenn N die zu übertragende Leistung in W ist und fu
in Hz eingesetzt wird.
Nach Auswahl eines passenden Bleches kann nunmehr auch die primäre Windungszahl np errechnet werden.
Hierfür gilt die folgende Formel

In dieser Gleichung ist l die in cm einzusetzende mittlere Weglänge der magnetischen Induktionslinien,
FK ist in cm² einzusetzen und ist in guter Annäherung an die in der Praxis gegebenen Verhältnisse
zu » 1000 einzusetzen; nach Errechnung von np ist zu prüfen, ob der
für µ angenommene Wert erreicht wird. Dabei ist naturgemäß Voraussetzung, daß für das benutzte
Blech entweder entsprechende Kurven oder Tabellen vorhanden sind.
Schließlich ist das einzuhaltende Übersetzungsverhältnis ü nach Formel 4 zu berechnen :

wobei ÂL der bei 800 Hz gemessene Wechselstromwiderstand des
Lautsprechers in W ist. Die sekundäre Windungszahl ns ergibt sich dann
nach der nächsten Formel.

Was die für die beiden Wicklungen zu verwendenden Drahtdurchmesser betrifft, so ist für die Primärwicklung
zumindest ein solcher Durchmesser zu wählen, daß die Stromdichte i möglichst nicht größer als
» 2,55 A/mm² wird; gegen einen größeren Durchmesser ist nichts einzuwenden, da dann
noch der Vorteil erhalten wird, daß der Spannungsabfall an der Primärwicklung sinkt. Die gleichen Gesichtspunkte
gelten naturgemäß auch hinsichtlich des Drahtdurchmessers für die Sekundärwicklung. Der in der
Sekundärwicklung zu erwartende Strom ergibt sich aus der zu übertragenden Wechselstromleistung und dem
Belastungswiderstand nach der nächsten Formel

in A, sofern N in W und ÂL in W
eingesetzt werden.
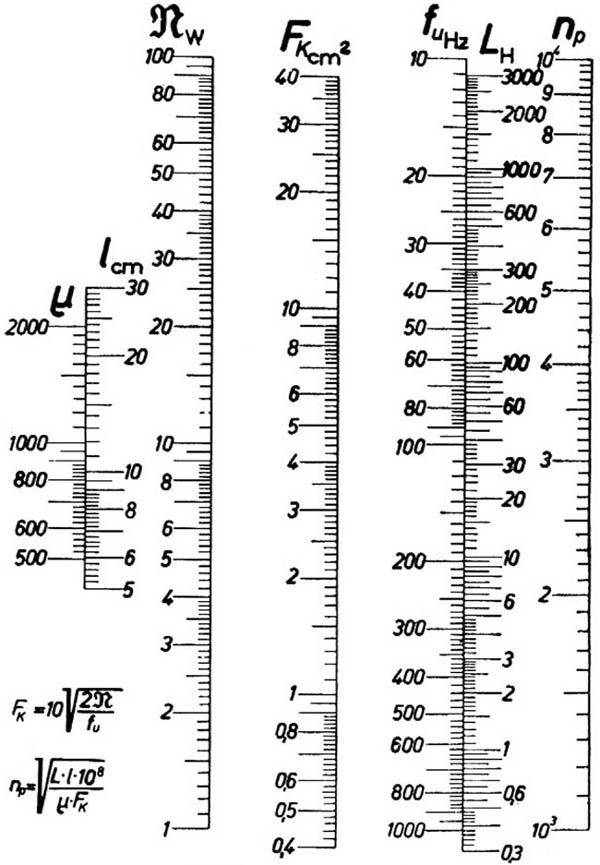
Die bisherigen Formeln können durch die nachfolgenden Nomogramme ersetzt werden.
Das erste Nomogramm gestattet die Ermittlung der für die Primärwicklung erforderlichen Induktivität L in
H, wenn fu die tiefste zu übertragende Frequenz ist. Davon abgesehen kann bei einem gegebenen
Ausgangstransformator bekannter Primär-Induktivität auch umgekehrt die tiefste noch übertragbare Frequenz
ermittelt werden. Die Anwendung des Nomogrammes soll an Hand eines Beispieles näher erläutert werden.
Beispiel:
Gegeben sei ein innerer Widerstand der benutzten Endröhre von Ri - 10 kW
und aus den Röhrenlisten geht hervor, daß Âa
gleichfalls 10 kW betragen soll. Wie groß muß die Induktivität L der
Primärwicklung gewählt werden, damit noch eine untere Frequenz fu von 100 Hz übertragen
wird, ohne daß sich ein nennenswerter Abfall bemerkbar macht?
Zunächst werden die für Ri und Âa
gegebenen Werte auf den betreffenden Leitern aufgesucht und durch eine Gerade miteinander verbunden. Der auf diese Weise auf
der Hilfsleiter H erhaltene Schnittpunkt (10,5) ist zu merken. Hierauf wird dieser Schnittpunkt mit dem für
fu gegebenen Wert - in unserem Beispiel also mit 100 Hz - durch eine weitere Gerade verbunden und wo
diese Gerade die L-Leiter schneidet, kann das gesuchte L unmittelbar abgelesen werden.
Im gewählten Beispiel ergibt sich auf diese Weise ein L von » 15 H.
Soll umgekehrt fu ermittelt werden, so wird in genau der gleichen Weise vorgegangen, nur mit dem
einzigen Unterschied, daß die zweite, von der Hilfsleiter H aus zu ziehende Gerade durch das jeweils gegebene L gelegt
und bis zur fu - Leiter verlängert wird, wo dann der gesuchte Wert abgelesen werden kann.
Dieses Nomogramm gestattet die Ermittlung des für die zu übertragende Leistung N bei der untersten Frequenz
fu in Betracht kommenden Eisenkern-Querschnittes FK sowie der Windungszahl
np der Primärwicklung zur Erzielung einer gegebenen Induktivität L bei den Werten n und I des
gegebenen Bleches. Beide Anwendungen sollen an Hand von Beispielen erläutert werden.
Beispiel:
Es soll eine Leistung N von 10 W bei einer untersten Frequenz fu von 100 Hz übertragen werden, wie
groß ist der Eisenkern-Querschnitt FK zu wählen?
Es sind lediglich die für N und fu gegebenen Werte aufzusuchen und durch eine Gerade miteinander
zu verbinden. Wo diese Gerade die Fk - Leiter schneidet, kann der gesuchte Eisenkern-Querschnitt
unmittelbar in cm² abgelesen werden. - Im Beispiel ergibt sich also FK zu 4,4 cm².
Beispiel:
Wie groß muß die primäre Windungszahl np gewählt werden, damit sich bei
FK = 4,4 cm², l = 12 cm und µ = 1000 eine Induktivität der Primärwicklung von
» 15 H ergibt?
Zunächst werden FK und µ durch eine Gerade miteinander verbunden, so daß sich auf der
N - Leiter ein Schnittpunkt ergibt, der zu merken ist. Dieser Schnittpunkt wird durch eine weitere Gerade mit dem für
l gegebenen Wert verbunden und diese Gerade bis zur FK - Leiter verlängert. Der Punkt, wo diese
zweite Gerade die FK - Leiter schneidet, wird durch eine weitere Gerade mit dem gegebenen L verbunden.
Die Verlängerung dieser Geraden bis zur rechten Leiter ergibt dort die gesuchte Primärwindungszahl
np zu » 2100.
Dieses dritte Nomogramm gestattet sowohl die Ermittlung des für bestimmte Werte von Âa und ÂL
einzuhaltenden Übersetzungsverhältnisses ü als auch die Bestimmung der sekundären Windungszahl
ns bei gegebener primärer Windungszahl np und gegebenem
Übersetzungsverhältnis ü. Auch die Anwendung dieses Nomogrammes soll wieder an entsprechenden Beispielen
gezeigt werden.
Beispiel:
Gegeben sei Âa zu 10 kW und ein
Wechselstromwiderstand des Lautsprechers bei 800 Hz von ÂL -
15 W. Wie groß ist das Übersetzungsverhältnis ü zu wählen?
Nachdem die für Âa und ÂL gegebenen Werte auf den beiden entsprechenden Leitern aufgesucht und durch eine
Gerade miteinander verbunden wurden, ergibt sich am Schnittpunkt der Leiter ü das gesuchte Übersetzungsverhältnis
zu 0,039.
Beispiel:
Wie groß ist die Sekundär-Windungszahl ns zu wählen, wenn eine Primär-Windungszahl
von 2100 gegeben ist und ein ü = 0,039 eingehalten werden soll?
Die für ü und np gegebenen Werte werden auf den entsprechenden Leitern aufgesucht und
durch eine Gerade miteinander verbunden. Am Schnittpunkt der Leiter ns kann dann die
gesuchte Sekundär-Windungszahl unmittelbar abgelesen werden. In unserem Beispiel ergibt sich ns
also zu » 80 Windungen.

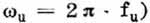 wesentliche Induktivität L der Primärwicklung des Ausgangstransformators errechnet sich nach der folgenden Formel
wesentliche Induktivität L der Primärwicklung des Ausgangstransformators errechnet sich nach der folgenden Formel